(Peer Reviewed) பசுவின் ரோமமும் குவாண்டம் கணிதமும்

ஸ்ரீ. நடராஜன் ஆற்றல் அறிவியல் துறை, அழகப்பா பல்கலைக்கழகம் காரைக்குடி மின்னஞ்சல்: natarajangravity@gmail.com இரெ. சந்திரமோகன் இயற்பியல் துறை, ஸ்ரீவித்யாகிரி கல்லூரி புதுவயல் மின்னஞ்சல்: rathinam.chandramohan@gmail.com
பசுவின் ரோமமும் குவாண்டம் கணிதமும்
முன்னுரை
நமது பழைய தமிழ்ப் பாடல்கள் அறிவியலைப் பற்றிப் பேசுகிறதா? முன்னோர்கள் அறிந்திருந்தனரா? என்பது போன்ற கேள்விகள் எப்போதும் விவாதிக்கப்பட்டுக் கொண்டே இருக்கின்றன. சமீபத்தில் கிடைத்த அறிவியல் வளர்ச்சியைப் பயன்படுத்தி மற்றும் சமீபத்தில் கிடைத்தத் தகவல்களைக் கொண்டு இப்பாடல்களை ஆராயும் போது சில வியத்தகு முடிவுகள் கிடைக்கின்றன. அவற்றை இக்கட்டுரையில் காணலாம்.
திருமந்திரப் பாடல்
திருமந்திரத்தில் அணுவைப் பற்றி பாடியுள்ள இரு பாடல்களை ஆய்விற்கு எடுத்துக் கொள்வோம்.
மேவிய சீவன் வடிவது சொல்லிடில்
கோவின் மயிரொன்று நூறுடன் கூறிட்டு
மேவியது கூறது ஆயிரமானால்
ஆவியின் கூறு நூறாயிரத்தொன்றாமே” [1]
பொருள் :
‘துறந்தார் பெருமை துணைக்கூறின் வையத்து, இறந்தாரை எண்ணிக்கொண்டற்று’ என்பதுபோல ஆருயிரின் வடிவம் அளவிட்டுக் கூறவொண்ணாததாகும். அவ்வுண்மையினை ஒருவகையாக ஓதியருள்வாராயினர். உடல் கலன் உலகம் ஊண் முதலியவற்றுடன் பொருந்திய ஆருயிரின் வடிவினைக் கூறுவோமானால் பசுவினது மயிர் ஒன்றினை எடுத்து நூறுபங்கு செய்தல்வேண்டும். பின்பு அந் நூற்றினில் ஒன்றினை எடுத்து ஆயிரம் கூறுசெய்தல்வேண்டும். அந் நிலையில் ஏற்படும் ஒரு கூற்றினை நூறாயிரம் கூறுசெய்தால் எவ்வளவு ஏற்படுமோ அவ்வளவாகும் ஆருயிரின் வடிவமென்க. எனவே, ஆருயிர்க்கு வடிவமின்றென்னும் வாய்மையினை வனப்புற வகுத்து ஓதுவதிது.
அணுவில் அணுவினை ஆதிப் பிரானை
அணுவில் அணுவினை ஆயிரங் கூறிட்டு
அணுவில் அணுவை அணுகவல் லார்கட்கு
அணுவில் அணுவை அணுகலு மாமே. [2]
பொருள்:
அணுவாகிய ஆருயிர்க்கு உயிராய் நுண்ணியனாய் விளங்குபவன் ஆதியாகிய அம்மையையுடைய சிவபெருமான் ஆவன். அவனைத் திருவருளுணர்வால் அளவின்றி நுணுகி ஆராயவல்லார்கட்கு அணுவுக்கு அணுவாய்த் திகழும் சிவபெருமானை அணுகுவது கைகூடும். இப்பாடல்களில் அணுவின் அளவு எவ்வளவு இருக்கும் என்பது பற்றிய கருத்துக்கள் தெரிவிக்கப்பட்டுள்ளன. இப்பாடலில் அணுவின் அளவானது பசுவின் ரோமத்தை அடிப்படையாகக் கொண்டு சொல்லப்பட்டுள்ளது. எனவே இப்பாடல் கூறும் அணுவின் அளவை ஆய்வு செய்வதற்குப் பசுவின் ரோமத்தை ஆய்வு செய்வதன் மூலம் தெளிவான விளக்கத்தைக் காண முடியும். இது போன்ற அடிப்படைத் துகள்களைப் பற்றி ஆராயும் போது அவற்றின் அளவுகளை மிகச்சரியாக சொல்லிவிட முடியுமா என்பது மற்றுமொரு ஆலோசனைக்குரிய விஷயம். ஏனென்றால் துகள்களின் அளவு மிகச் சிறியதாகச் செல்லச் செல்லக் குவாண்டம் விளைவுகள் அதிகமாக இருக்கும். இவ்வகையான விளைவுகள் குவாண்டம் நிலையில்லாத் தத்துவத்தின் மூலம் நிரூபிக்கப்படுகின்றன. நிலையில்லாத் தத்துவம் என்பது ஒரு துகளின் இருப்பினையும் மற்றும் அதன் உந்தத்தையும் இணைக்கிறது. இதன் மூலம் தெரிய வருவது என்னவென்றால் குவாண்டம் துகள்களின் இயக்கத்தை ஆராயும்போது ஒரே நேரத்தில் துகள்களின் இருப்பினையும் மற்றும் உந்தத்தினையும் ஒருசேரக் கணக்கிட இயலாது என்பதாகும். அதாவது துகளின் இருப்பினை ஆராய வேண்டுமானால், அது உந்தத்தில் சார்பாக இருக்கும். இதேபோல உந்தத்தை ஆராய வேண்டுமானால் அது இருப்பின் சார்பாக இருக்கும். இவற்றைக் கீழ்காணும் சமன்பாடு மூலம் இணைக்க முடியும்.
மேலும் இதே தத்துவத்தின் விளைவானது துகள்களின் அளவை ஆராயும்போது பாதிப்பை ஏற்படுத்தும். எவ்வாறெனில் அடிப்படைத் துகள்களின் அளவினை ஆராயும் போது அதன் உந்தமும் பெருமளவில் இந்த ஆய்வின் விளைவைப் பாதிக்கும். எனவே அடிப்படைத் துகளின் குறுக்களவினை மிகச் சரியாக அளவிட முடியாது.
பசுவின் ரோமம்
அடிப்படைத் துகள்களில் ஒன்றான எலக்ட்ரானின் வடிவமைப்பைச் சமீபத்திய ஆய்வு ஒன்று உறுதி செய்துள்ளது [4]. கிட்டத்தட்ட 10 ஆண்டுகாலம் மேற்கொள்ளப்பட்ட அவ்வாய்வின் முடிவில் எலக்ட்ரானானது ஒப்பீட்டளவில் ஒரு கோள வடிவமான அமைப்பைப் பெற்றிருக்கும் என்று கண்டறியப்பட்டுள்ளது. இந்த ஆய்வுக்கு மிக குளிர்ந்த சூழ்நிலையானது ஏற்படுத்தப்பட்டது. இங்கு வெப்பநிலையானது 3 கெல்வின் என்ற அளவில் குளிர்ந்த நிலையில் இருக்கும் [4]. இதன்மூலம் அடிப்படைத் துகள்களின் இயக்கம் மட்டுப்படுத்தப்பட்டு அவற்றின் அமைப்புகள் ஆய்வு செய்யப்பட்டன.
இப்பாடலில் உள்ள கருத்துக்களை உறுதிசெய்ய பசுவின் ரோமத்தின் குறுக்களவானது ஆய்வகத்தில் கணக்கிடப்பட்டது. இந்த ஆய்வுக்காக பத்து பசு மாடுகளில் ரோமங்கள் சேகரிக்கப்பட்டது. அவ்வாறு பெறப்பட்ட ரோமங்கள் ஆய்வகத்திற்குக் கொண்டு வரப்பட்டு அவற்றின் குறுக்களவானது கண்டறியப்பட்டன. ஏர்வெட்ஜ் முறையில் ரோமத்தின் குறுக்களவானது அளவிடப்பட்டது. இவ்வாறு பெறப்பட்ட தரவுகள் ஏற்கனவே உள்ள ஆய்வு முடிவுகளுடன் ஒப்பிட்டுப் பார்க்கப்பட்டது [3].
உரோமத்தின் குறுக்களவு பின்வரும் சமன்பாட்டின் மூலம் பெறப்படுகிறது.
L என்பது கண்ணாடித் தட்டின் எல்லையிலிருந்து உரோமமானது வைக்கப்பட்டுள்ள நீளத்தையும், D என்பது கண்ணாடித் தட்டின் குறுக்களவையும், என்பது மஞ்சள் நிறத்தின் அலைநீளத்தையும், என்பது ஒளிவிலகல் எண்ணையும் மற்றும் N என்பது ஒளிப்பட்டைகளின் எண்ணிக்கையையும் குறிக்கும். எமது ஆய்வுத்தரவுகளில் பின்வரும் மதிப்புகள் அடிப்படையாகக் கையாளப்பட்டன.
இவ்வாறு பெறப்பட்ட மதிப்புகளை குறுக்களவு சமன்பாட்டில் பிரதியிட, கிடைக்கும் எண்மதிப்பு உரோமத்தின் குறுக்களவை உறுதி செய்கிறது.
இப்பகுதியானது பாடலின் வரியையும் மற்றும் கணக்கீடுகளையும் ஒப்பிட்டு விளக்குகிறது. நாம் கண்டுபிடித்த ரோமத்தின் குறுக்களவை அடிப்படையாகக் கொண்டு இக்கணக்கீடுகள் செய்யப்படுகின்றன. பசுவின் ரோமம் குறுக்களவு = 160 மைக்ரோ மீட்டர்
முதல் வரி
இரண்டாவது வரி
மூன்றாவது வரி
4 வது வரி
இவ்வாறு கிடைக்கப்பட்ட எண் மதிப்பின் அளவை அறிவியல் தரவுகளுடன் ஒப்பிடும்போது சில ஒப்பீட்டளவிலான முடிவுகள் கிடைக்கின்றன. இங்கு கிடைக்கப்பட்ட மதிப்பான 160 x 10^-16 மீட்டர் என்ற எண் மதிப்பானது ஒரு ஹைட்ரஜன் அணுவை விட மிகக் குறுகியது. ஹைட்ரஜன் அணுவானது 53 x 10^-12 மீட்டர்கள் என்ற எண் மதிப்பைக் குறுக்களவாகப் பெற்றிருக்கும். எனவே இங்கு குறிப்பிட்டுள்ள அடிப்படைத்துகளின் அளவு என்பது இந்த ஹைட்ரஜன் அணுக்களை விடவும் மிகச் சிறியதாக இருக்கும்.
குவாண்டம் தத்துவம்
குவாண்டம் இயற்பியலைப் பொருத்தவரையில் நிகழ்தகவு விளையாட்டுகளின் அடிப்படையில் தத்துவங்கள் கட்டமைக்கப்பட்டுள்ளன. குவாண்டம் இயற்பியலில் ஒரு துகளின் இருப்பை நிகழ்தகவு அடிப்படையில் வெளிப்படுத்த முடியும். இதற்குப் பின்னணியில் ஹெய்சன்பர்க்கின் நிலையில்லாத் தத்துவம் வேலை செய்கிறது. நிலையில்லாத் தத்துவத்தின்படி, இயங்கும் நிலையில் இருக்கும் ஒரு துகளின் இருப்பினையோ அல்லது உந்தத்தையோ ஒரு சேர அறுதியிட்டுக் கூற முடியாது.
அவ்வாறெனில் துகள்களில் இயக்கத்தை எவ்வாறு கணக்கிடுவது? இந்த சிக்கலைத் தீர்க்க, நிகழ்தகவின் கணம் என்ற சமன்பாட்டுத் தொடர்பு பயன்படுத்தப்படுகிறது. இவ்வகையான சமன்பாடுகளில் அலைச்சார்பு என்பது பயன்படுத்தப்படுகிறது. இதன் காரணம், அடிப்படை நிலையில் பருப்பொருளானது, அலையாகவும், துகளாகவும் இயங்கி வருவதைக் குவாண்டம் இயற்பியல் விதிகள் வெளிப்படுத்துகின்றன. அலைச் சார்பு என்பது இயங்கும் ஒரு துகளின் நிலையும், நேரத்தையும் இணைத்துக்கொண்ட ஒரு பொதுச்சார்பாக வரையறுக்கப்படுகிறது.
இதனை அடிப்படையாகக் கொண்டு துகள் ஒன்றின் நிகழ்தகவுக் கணத்தை வரையறுக்க முடியும். ஒரு துகளின் நிகழ்தகவுக் கணம் என்பது அதன் அலைச்சார்பு மற்றும் அதன் கலப்பு இணை ஆகியவற்றின் பெருக்கத் தொகைக்கு நேர்த்தகவில் இருக்கும்
இந்த நிகழ்வுகளில் கணத்தை அலைசார்புடன் இயல்பாக்கும் செயல்முறைக்குத் (normalization) தலைப்படும் போது பின்வருமாறு மதிப்புகள் கிடைக்கிறது.
நிகழ்தகவின் தற்போதைய கணம் என்பது, குவாண்டம் இயற்பியலின் ஷ்ரோடிங்கர் சமன்பாட்டை மாற்றியமைப்பதன் மூலம் பெறப்படுகிறது.
குவாண்டம் இயற்பியல் ஆனது ஹில்பர்ட் வெளியில் கட்டமைக்கப்படுகிறது. ஹில்பர்ட் வெளியானது முடிவுறாப் பரிமாணங்களைக் கொண்டது. இதன்மூலம் தொன்மை இயற்பியலில் உள்ள முப்பரிமாண வெளியைத் தாண்டிய அதிகமான பரிமாணங்களில், சமன்பாடுகளை எழுத இயலும். மேலும் இவ்வெளியானது துகள் மற்றும் அலை சார்ந்த சமன்பாடுகளை எழுதுவதற்கு அதிக சுதந்திரத்தைத் தருகிறது.
குவாண்டம் இயற்பியலின் எதிர்பார்ப்பு மதிப்புகள்
குவாண்டம் இயற்பியலைப் பொருத்தவரையில் ஒரு துகளின் இருப்பையும், அதன் நேரத்தையும் இணைத்து நிகழ்தகவின் கணம் என்ற சமன்பாடு ஒன்றிணைப்பது குறித்துப் பார்த்திருந்தோம். நிகழ்தகவின் கணம் என்பது ஒரு துகள் ஆனது ஒரு குறிப்பிட்ட வெளி அளவில் மற்றும் இருக்கக்கூடிய மொத்த நேரங்களின் அமைப்பில் பரவியிருக்கும் நிகழ்தகவின் மொத்த எண்மதிப்பை அளவிடுகிறது. அவ்வாறெனில் ஒரு துகளின் அடிப்படை அளவை நாம் அறுதியிட்டு கூற முடியாதா? என்ற ஒரு கேள்வி எழுப்பலாம்.
அதற்கு பதிலாக எதிர்பார்ப்பின் எண்மதிப்பு என்ற மாபெரும் விடையானது கிடைக்கிறது. எதிர்பார்ப்பின் எண்மதிப்பு என்பது நிகழ்தகவுக் கணங்களை, நாம் எதிர்பார்க்கும் நிலைப்பள்ளியில் தொகுக்கக் கிடைக்கும் எண்மதிப்பைப் பெற்றிருக்கும். அவற்றை சமன்பாடு வாயிலாக கீழ்கண்டவாறு எழுதலாம்.
மொத்த ஆற்றலின் எதிர்பார்த்தல் எண் மதிப்பானது பின்வருமாறு கணக்கிடப்படுகிறது. எண்மதிப்பானது நிலை ஆற்றலின் எதிர்பார்த்தல் மதிப்பிற்கும் இயக்க ஆற்றலின் எதிர்பார்த்தல் மதிப்பிற்கும் உண்டான கூட்டுத் தொகைக்குச் சமமாக இருக்கும்.
உந்தத்தின் எதிர்பார்த்தல் மதிப்பானது பின்வருமாறு எழுதப்படுகிறது.
எஃரன்பெஸ்ட் விதியானது திசை வேகத்தையும் உந்தத்தையும் ஒருங்கிணைப்பது போல், விசையையும் நிலையாற்றலையும் ஒருங்கிணைக்கிறது.
இவற்றின் விளைவாக எண்ணற்ற சிக்கல்களை தீர்த்துக் கொள்ள முடியும். சரி தற்போது இந்த கேள்விக்கு வருவோம். திருமந்திரம் சொல்லும் உயிர் பற்றிய அளவீடு குறித்து குவாண்டம் இயற்பியல் எவ்வாறு தனது கணக்கீடுகளை முன்வைக்கிறது? என்று இயற்பியலின் தலைசிறந்த கோட்பாட்டின் மீது நாம் கேள்வி எழுப்பலாம்.
தற்போது நாம் மேலே குறிப்பிட்டுள்ள அலைச்சார்பு குறித்த தகவல்களின் மூலமும், எதிர்பார்ப்பின் கணம் என்ற சமன்பாட்டின் மூலமும் மேலே உள்ள கேள்வியைப் பற்றி விரிவாக ஆய்வு செய்யலாம். இதன் அடிப்படையில் நாம் பார்க்கும்போது ஒரு துகள் ஒரு குறிப்பிட்ட இடத்தில் இருப்பது என்பதை ஆராய்வது என்பது அதன் நிகழ்தகவுக் கணங்களில் மதிப்பைப் பொறுத்து அமையும்.
இதனடிப்படையில் ஒரு துகளின் அளவானது அளவிடப்பட வேண்டும் வேண்டுமென்றால் அந்த கணக்கீடானது நிகழ் தகவுகளின் அடிப்படையிலேயே கட்டமைக்கப்படும். மேலும் குவாண்டம் இயற்பியல் அடிப்படைத்துகள்களை அலைத்துகள் கோட்பாட்டின் மூலம் ஆய்வு செய்கிறது. இக் கோட்பாட்டின்படி அதிக உந்தம் கொண்ட துகள்கள், குறைந்த அலைநீளம் கொண்டதாகச் செயல்படும் . இதன் விளைவாகத் திருமூலர் பாடலில் சொல்லியுள்ள மிகக் குறுகிய அளவிலான துகள்களை ஆய்வு செய்ய முற்படுகையில் அவற்றின் உந்தமானது மிக அதிகமாக இருக்கும் என்பதைக் கண்டறிய முடியும்.
அத்தகைய துகள்களை ஆய்வு செய்ய வேண்டுமானால் மிக அதிக திறன் கொண்ட துகள் முடுக்கிகள் தேவைப்படும். எனவே திருமூலர் பாடலில் சொல்லியுள்ள உயிரின் அளவு குறித்த மதிப்பை நிகழ்தகவு கணங்களின் மதிப்பீடுகளில், தொடர் மதிப்புகளில் ஒரு நிகழ்தகவு எண்மதிப்பாக கருத்தில் எடுத்துக் கொள்ளலாம். எலக்ட்ரானின் தொன்மை ஆரம் என்பதைக் கீழ்வரும் சமன்பாடு மூலம் கணக்கிடலாம்.
இவ்வாறு பெறப்படும் எண் மதிப்பு 2.82 x 10^-15 மீட்டர் என்ற எண் மதிப்பைப் பெற்றிருக்கும். மேலும் நமது கணக்கின் மூலம் கிடைக்கும் எண் மதிப்பானது, எலக்ட்ரானின் அளவைவிட சற்றுச் சிறிதாகவே உள்ளது. இது எலக்ட்ரானின் அலைச்சார்பு மூலம் பெறப்படுகிறது.
முடிவுரை
எலக்ட்ரானின் குறுக்களவு நேரடியாக மதிப்பிடப்பட இயலாது. காரணம் குவாண்டம் அளவில் அடிப்படைத் துகள்களானவை ஒரே சமயத்தில் துகளாகவும் அலையாகவும் பரிணமிக்கும். இவ்வெண் மதிப்பானது எலக்ட்ரானின் அலைச்சார்பு மூலம், நிலையில்லாக் கோட்பாட்டை அடிப்படையாகக் கொண்டு பெறப்படுகிறது. தொன்மை இயற்பியலைப் பொருத்தவரை அறுதியிட்டு கூறப்படும் எண்மதிப்புகள் குவாண்டம் இயற்பியலில் நிகழ்தகவுக் கணங்களாக மாற்றப்படுவதால் நம்மால் ஒரு துகளின் அளவை அறுதியிட்டுக் கூறமுடியாது. எனவே இப்பாடலில் குறித்துள்ள ஆவியின் அளவு என்பதை நிகழ்தகவுக் கணங்களில் தொகுப்பாகவே நாம் எடுத்துக்கொள்ள வேண்டும். இப்பாடல் அணுவின் அளவு என்பது குறித்து விளக்கியிருந்தாலும், கணக்கீடுகளின் படி இப்பாடல் சொல்ல விழையும் அணு என்னும் கருத்து அடிப்படைத்துகள்களையே குறிக்கிறது என்று யூகிக்க முடிகிறது. எனவேதான் ஆவி என்னும் சொல்லாடலை அணு என்னும் சொல்லாடலுடன் இணைத்துப் பயன்படுத்தியுள்ளோம். திருமூலருக்கு குவாண்டம் இயற்பியல் தெரிந்திருக்குமா என்ற கேள்விக்கு இக்கட்டுரை செல்லவில்லை. மாறாக அவர் சொல்லும் கருத்தை குவாண்டம் இயற்பியலில் ஏற்றி விளக்க முற்பட்டுள்ளது. இதன் மூலம் தமிழின் தொன்மைத்தன்மைகளை நாம் நவீன இயற்பியலில் மூலம் ஆய்வு செய்யும்போது பல்வேறு தகவல்கள் புரிய வருகிறது, என்பதை உணர்ந்து கொள்ள முடியும். இது போன்ற பல்வேறு கணக்கீடுகள் தமிழில் பல்வேறு நூல்களில் பொதிந்திருக்கும். அவற்றை ஆராய வேண்டியது ஆய்வாளர்களின் கடமை.
ஆதாரங்கள்
[1] திருமூலர், திருமந்திரம், சீவன், பா.2011
[2] திருமூலர், திருமந்திரம், பசு இலக்கணம், பா.1
[3] Kshirsagar, S. V., Singh, B., & Fulari, S. P. (2009). Comparative study of human and animal hair in relation with diameter and medullary index. Indian Journal of Forensic Medicine and Pathology, 2(3), 105-8.
[4] Hudson, J. J., Kara, D. M., Smallman, I. J., Sauer, B. E., Tarbutt, M. R., & Hinds, E. A. (2011). Improved measurement of the shape of the electron. Nature, 473 (7348) 493.
ஆய்வறிஞர் கருத்துரை (Peer Review):
இந்த ஆய்வுக் கட்டுரையானது, திருமந்திரப் பாடல் வரிகளை குவாண்டம் அறிவியலுடன் ஒப்பிட்டு விவரிக்கிறது. சில ஆய்வகச் சோதனைகளும், உசாத்துணைகளும் கட்டுரையில் கூறப்பட்டுள்ள கருத்துகளுக்கு வலுச் சேர்ப்பதாக அமைந்திருக்கின்றன. தமிழ் இலக்கியங்களில் பொதிந்துள்ள அறிவியல் கருத்துகளை ஆய்வக சோதனைகள் மூலம் வெளிக்கொணரும் முயற்சிகள் பரவலாக மேலெழுவதற்கு இக்கட்டுரை தொடக்கப் புள்ளியாக அமையும் என்பதில் ஐயம் இல்லை.


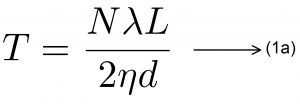
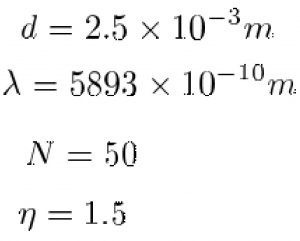
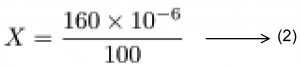
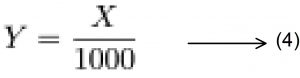


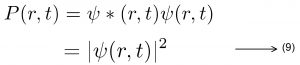
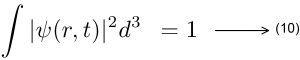
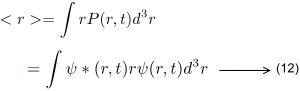
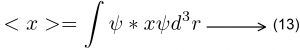
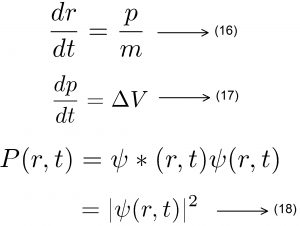
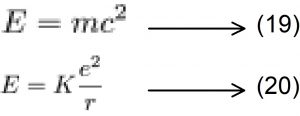







மிகவும் ஆய்சிரியம் கொடுக்கும் பதிவு.. நன்றி
அருமை. ஆராய்ச்சி தொடரட்டும், விரிவடையட்டும், வெற்றிபெறட்டும்.
வாழ்த்துக்கள்